La numération
Le but de ce cours est de voir l’essentiel pour faire le MOOC à propos de la numération. On ne parlera que des bases 2, 8, 10 et 16 et plus particulièrement que des entiers relatifs. Pour ne pas avoir de confusion, la valeur se note entre crochets et le nombre à droite des crochets indique dans quelle base est cette valeur (exemple: [1E]16, [01001001]2)
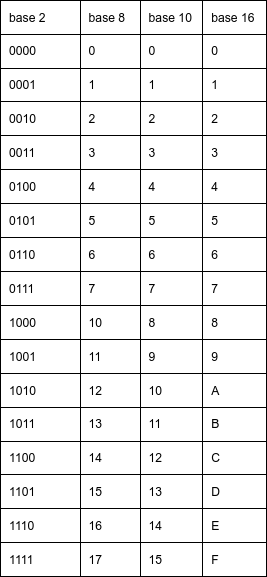
I) Valeurs remarquables
II) Conversion
1) base 10 vers les autres
Il suffit de faire des divisions euclidiennes successives par la base qui nous intéresse.
Par exemple : [25]10 en base 2 :
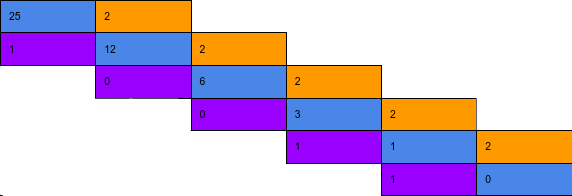
Pour bien comprendre cette suite de divisions, il vaut voir une étape comme l'image qui suit :
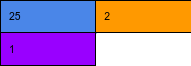
Avec la légénde :

Une fois que le reste qui devient dividende vaut 0 il faut lire les restes de droite à gauche de bas en haut. Si on suit cette méthode on obtient [11001]2 avec l’exemple.
2) Autres bases vars base 10
Pour passer d'une base quelconque vers la base 10 il faut multiplier le chiffre par la valeur de la base de départ à l'exposant correspondant à la position du chiffre dans le nombre (poids) et ensuite l'ajouter aux autres chiffres. La numérotation des poids se fait de droite à gauche et commence à 0.

Comme on peut le voir dans l'image ci-dessus on veut convertir [1A5E]16 en base 10. Attention la plupart des calculatrices ne savant pas gérer l'écriture Hexadécimale, il faut traduire les valeurs numériques écrites avec des lettres. Pour ce faire il faut calculer la valeur de :
1*16^3 + 10*16^2 + 5*16^1 + 14*16^0 ce qui donne [6750]10
3) Cas particuliers
Il est à noter que l'on peut passer facilement de la base 2 vers la base 8 ou 16 et inversement en utilisant les valeurs remarquables vues en I)
Pour passer des bases 16 et 8 vers la base 2 il suffit de remplacer chaque chiffre (ou lettre) par sa valeur en base 2 comme vu dans le point II)3). Par exemple [164]8 donne [0001 0110 0100]2 et [164]16 donne [0001 0110 0100]2. Les 0 à gauche du nombre ne sont pas obligatoires mais sont là à titre pédagogique.
Pour passer de la base 2 vers les bases 16 et 8 on regroupe les chiffres par paquets de 4 en partant de la droite. De même que pour la conversion précédente, les 0 à gauche ne sont pas obligatoires on peut les rajouter pour compléter le dernier groupe de 4. On appelle un groupe de 4 chiffres un quartet et un groupe de 8 chiffres un octet.